
怎么对数据进行排序?排序算法有多种,该使用哪种排序算法呢?回顾下时间复杂度较低的归并排序
归并排序
归并排序的核心分为两个部分。1。将待排序数据对半分,直到只剩一个元素。2。针对两部分的数据(每部分已经是有序的)进行排序,左半部分与右半部分进行排序
归并排序(递归方式)
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| public void mergeSortByRecursive(int[] data) {
long startTime = System.nanoTime();
mergeSortRecursive(0, data.length - 1, data, new int[data.length]);
System.out.println("MergeSortRecursive Time Cost : " + (System.nanoTime() - startTime) * 0.000001 +" ms");
checkSortedData(data,"MergeSortRecursive");
}
private void mergeSortRecursive(int lowIndex, int highIndex, int[] data, int[] temp) {
if (lowIndex >= highIndex) {
return;
}
int mid = ((highIndex - lowIndex) >> 1) + lowIndex;
int startOne = lowIndex, endOne = mid, startTwo = mid + 1, endTwo = highIndex;
mergeSortRecursive(startOne, endOne, data, temp);
mergeSortRecursive(startTwo, endTwo, data, temp);
mergeData(lowIndex, mid, highIndex, data, temp);
}
private void mergeData(int lowIndex, int middle, int highIndex, int[] data, int[] temp) {
for (int i = lowIndex; i <= highIndex; i++) {
temp[i] = data[i];
}
int leftStart = lowIndex, rightStart = middle + 1;
int tempIndex = leftStart;
while (leftStart <= middle && rightStart <= highIndex) {
data[tempIndex++] = temp[leftStart] < temp[rightStart] ? temp[leftStart++] : temp[rightStart++];
}
while (leftStart <= middle) {
data[tempIndex++] = temp[leftStart++];
}
}
|
递归归并排序示意图
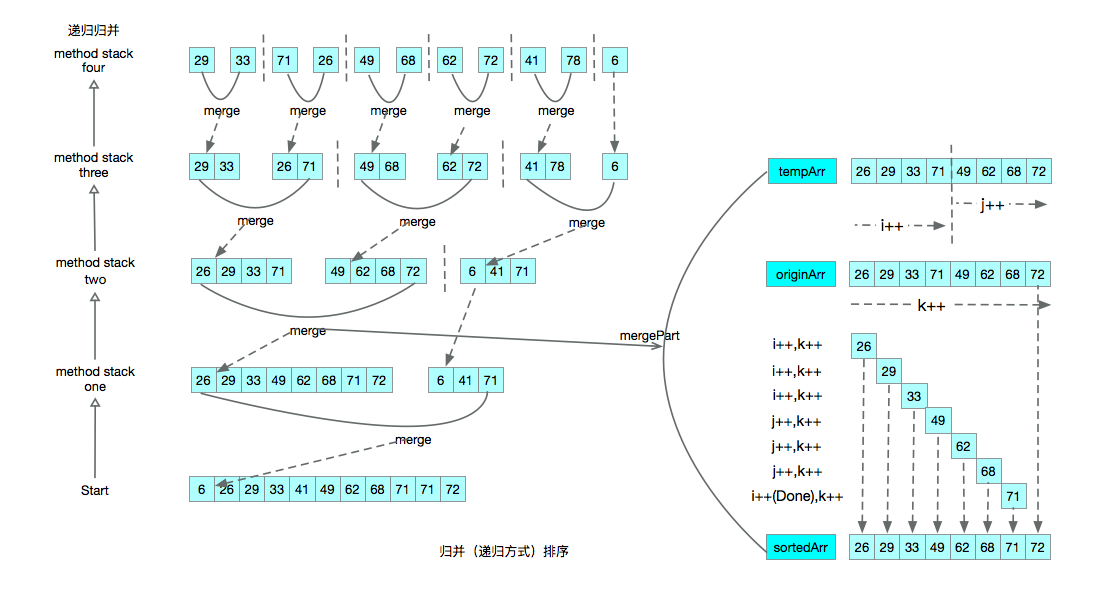
上述的排序代码是理想状态下的,当排序的数据量较大的时候,1。使用递归的方式对数据进行分治,排序的过程将不能正常结束,递归达到一定的深度将导致栈内存溢出。2。merge排序过程中需要额外的存储空间
归并排序(迭代方式)
迭代归并排序将不会出现栈内存溢出的问题,同时对于merge部分可以采用原地排序,降低空间复杂度
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| private void mergeSortByIterative(int[] data) {
for ( int block=1; block<=data.length-1/2; block = 2*block)
{
for (int left_start=0; left_start<data.length-1; left_start += 2*block)
{
int mid = left_start + block - 1 < data.length-1 ? left_start + block - 1 : left_start-1;
int right_end = (left_start + 2 * block - 1) < data.length - 1 ? left_start + 2 * block - 1 : data.length-1;
mergeDataInPlace(left_start,mid,right_end,data);
}
}
}
private void mergeDataInPlace(int lowIndex, int middle, int highIndex, int[] data) {
int i = lowIndex;
int j = middle + 1;
while(i < j && j <= highIndex)
{
while(i < j && data[i] <= data[j])
{
i++;
}
int index = j;
while(j <= highIndex && data[j] <= data[i])
{
j++;
}
swap(data, i, index-i, j-index);
i += (j-index);
}
}
private void swap(int arr[], int i, int k, int j) {
reverse(arr, i, i + k - 1);
reverse(arr, i + k, i + k + j - 1);
reverse(arr, i, i + k + j - 1);
}
private void reverse(int[] arr, int i, int j) {
while(i < j)
{
arr[i] ^= arr[j];
arr[j] ^= arr[i];
arr[i] ^= arr[j];
i++;
j--;
}
}
|
迭代归并排序示意图
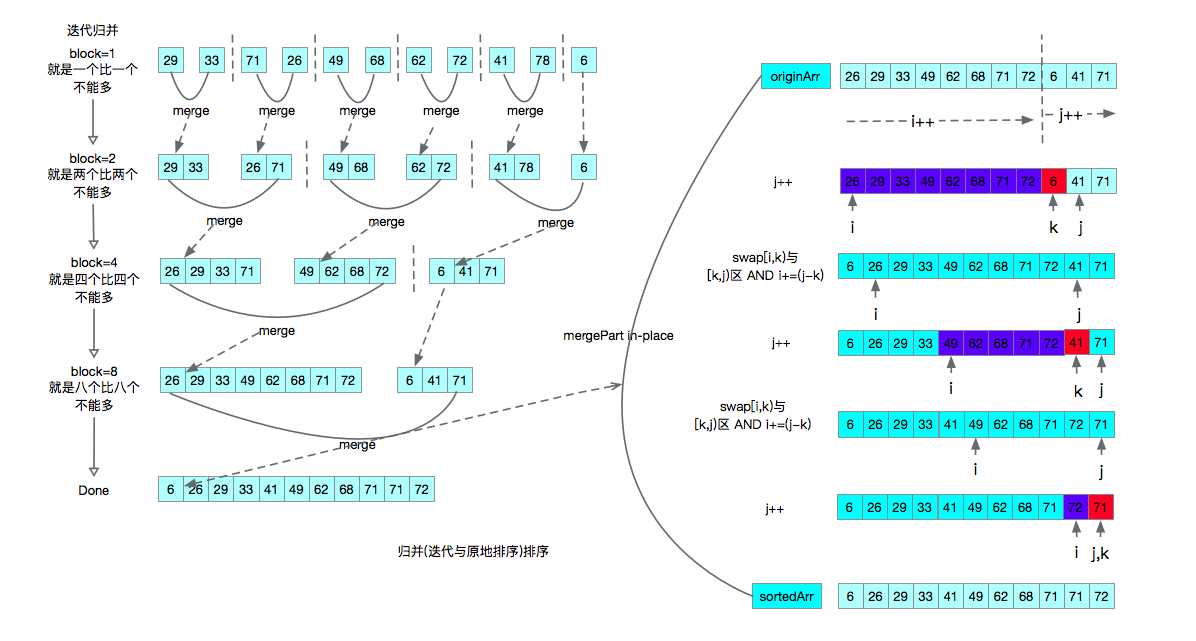
归并的算法复杂度
- 将N个待排序的数据对半分,分到剩下单个元素为止,这个过程需要log2N次
- 针对两部分有序的数据进行排序,比较的次数介于 N ~ N/2 之间
- 时间复杂度:O(Nlog2N)
- 空间复杂度:O(1) ~ O(N)
实际运行效果
时间与空间不可兼得
来看看归并排序具体所需的时间,测试数据为0~20W的随机大小数字,20W个数据排序5次
| 排序次数 |
所需时间 |
| 1 |
20093.858586 ms |
| 2 |
19864.726974999998 ms |
| 3 |
19930.830952 ms |
| 4 |
19667.228037999997 ms |
| 5 |
19873.263419 ms |
| 排序次数 |
所需时间 |
| 1 |
69.183775 ms |
| 2 |
45.25653 ms |
| 3 |
36.282312 ms |
| 4 |
38.270578 ms |
| 5 |
35.130196999999995 ms |
merge部分算法不同,排序的整体时间天壤之别。。。In-Place merge虽然节省了空间,但是带来了更多的元素移动,更多的时间消耗。时间复杂度与空间复杂度不可兼得
Fork/Join排序
来看看对千万级的数据量进行排序,时间情况如何。测试数据1000W
| 排序次数 |
所需时间 |
| 1 |
2690.39711 ms |
| 2 |
2267.34402 ms |
| 3 |
2423.867487 ms |
| 4 |
2543.747986 ms |
| 5 |
2409.55724 ms |
归并排序先把大量的数据分为多个小量的数据(分治),然后合并小量的数据(合并),这不是在说Fork/Join的嘛,而且Fork/Join可以利用多核,那么利用Fork/Join排序会不会快一点?
| 排序次数 |
所需时间 |
| 1 |
10921.404759 ms |
| 2 |
16899.215443 ms |
| 3 |
14746.151189 ms |
| 4 |
14887.626859999998 ms |
| 5 |
15565.447017999999 ms |
不敢相信的速度,Fork/Join排序会消耗大量的内存空间,导致频繁的GC,归并排序分治的最小任务是1,Fork/Join虽能并行的处理排序,但任务如果分的过小,会带来更多的线程切换,相比单线程的迭代归并排序,反而需要更多的时间
I’m not a devil, I’m just a good man, put in a bad place. - Verbal Kint
The Usual Suspects


